


I am a mathematician interested in basic and applied research questions that arise in the contexts of geometric mechanics, data science, nonlinear PDEs, and scientific machine learning.
Lately, my focus is primarily on developing structure-informed numerical methods for scientific applications. Doing this generally involves identifying or reasoning about some abstract mathematical structure which is important for a particular physical phenomenon, formulating a smart discretization (based on, e.g., a finite element or artificial neural network backbone) which takes this structure into account, and writing mathematical software in Python or C++ which implements a proposed approach. Over time, I’ve found that my preferred flavor of research problem leaves ample opportunity for geometric ideas, satisfying visuals, and punchy algebraic arguments which are characteristic of my personal style.
More about me
A differential geometer by training, I received my PhD from Texas Tech University under the guidance of Magdalena Toda, with co-advisors Eugenio Aulisa and Hung Tran. At this time, I applied techniques from Riemannian geometry, variational calculus, and differential topology to study functionals involving surface curvature, with the ultimate goal of understanding their extrema. Moreover, I was (and still am) interested in understanding the possible immersions of a given topological space inside another, including what configurations are “preferred” (usually energy-minimizing) in this case. I also spent quite a bit of time thinking about the computational modeling of geometric objects, sparking a standing interest in computer graphics which can be seen in the various simulation videos found on the Gallery page.
Catalyzed by an NSF internship at Oak Ridge National Lab (featured here!) toward the end of graduate school where I worked with Robert Bridges, I became involved post-PhD in scientific algorithm development for dimension reduction, function approximation, and the reduced-order modeling of PDEs. This led to a postdoctoral appointment with Max Gunzburger at FSU working on data-driven strategies for predictive tasks related to ocean modeling. At the same time as my application-driven interests were shifting, my purer “side project” work also moved in the direction of rigidity results for geometric objects constrained by curvature conditions. Now, I maintain active interests in several areas of mathematics, computer science, and engineering.
Broad research keywords which tend to interest me include: scientific machine learning, computational and discrete geometry, conservation laws, reduced-order modeling, manifold learning, harmonic maps, surface immersions, and integrability problems.

Below are some coarse categories containing (some of) my work. Some have their own page for further reading. (This part of the website is a work-in-progress.)
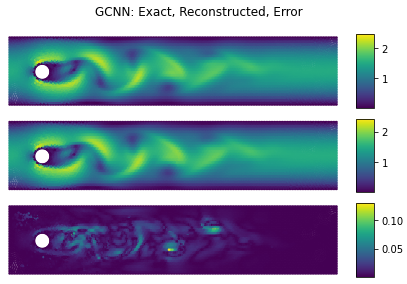 Due to their high computational cost, scientific studies based on large-scale simulation frequently operate at a data deficit which creates problems inverse to the issues with “big data”. Particularly, there is a need for efficient function approximation and model reduction strategies which can serve as cheap and reliable surrogates for the high-fidelity models used in practical applications. These projects develop such technology using invariances and other structural considerations as a starting point, allowing for informed surrogates with beneficial behavior.
Due to their high computational cost, scientific studies based on large-scale simulation frequently operate at a data deficit which creates problems inverse to the issues with “big data”. Particularly, there is a need for efficient function approximation and model reduction strategies which can serve as cheap and reliable surrogates for the high-fidelity models used in practical applications. These projects develop such technology using invariances and other structural considerations as a starting point, allowing for informed surrogates with beneficial behavior.
Projects
Tensor Parametric Hamiltonian Operator Inference Preprint
 Abstract: TThis work presents a tensor-based approach to constructing data-driven reduced-order models corresponding to semi-discrete partial differential equations with canonical Hamiltonian structure. By expressing parameter-varying operators with affine dependence as contractions of a generalized parameter vector against a constant tensor, this method leverages the operator inference framework to capture parametric dependence in the learned reduced-order model via the solution to a convex, least-squares optimization problem. This leads to a concise and straightforward implementation which compactifies previous parametric operator inference approaches and directly extends to learning parametric operators with symmetry constraints, a key feature required for constructing structure-preserving surrogates of Hamiltonian systems. The proposed approach is demonstrated on both a (non-Hamiltonian) heat equation with variable diffusion coefficient as well as a Hamiltonian wave equation with variable wave speed.
Abstract: TThis work presents a tensor-based approach to constructing data-driven reduced-order models corresponding to semi-discrete partial differential equations with canonical Hamiltonian structure. By expressing parameter-varying operators with affine dependence as contractions of a generalized parameter vector against a constant tensor, this method leverages the operator inference framework to capture parametric dependence in the learned reduced-order model via the solution to a convex, least-squares optimization problem. This leads to a concise and straightforward implementation which compactifies previous parametric operator inference approaches and directly extends to learning parametric operators with symmetry constraints, a key feature required for constructing structure-preserving surrogates of Hamiltonian systems. The proposed approach is demonstrated on both a (non-Hamiltonian) heat equation with variable diffusion coefficient as well as a Hamiltonian wave equation with variable wave speed.
(Joint with Arjun Vijaywargia and Shane A. McQuarrie.)
Efficiently Parameterized Neural Metriplectic Systems Preprint
 Abstract: Metriplectic systems are learned from data in a way that scales quadratically in both the size of the state and the rank of the metriplectic data. Besides being provably energy conserving and entropy stable, the proposed approach comes with approximation results demonstrating its ability to accurately learn metriplectic dynamics from data as well as an error estimate indicating its potential for generalization to unseen timescales when approximation error is low. Examples are provided which illustrate performance in the presence of both full state information as well as when entropic variables are unknown, confirming that the proposed approach exhibits superior accuracy and scalability without compromising on model expressivity.
Abstract: Metriplectic systems are learned from data in a way that scales quadratically in both the size of the state and the rank of the metriplectic data. Besides being provably energy conserving and entropy stable, the proposed approach comes with approximation results demonstrating its ability to accurately learn metriplectic dynamics from data as well as an error estimate indicating its potential for generalization to unseen timescales when approximation error is low. Examples are provided which illustrate performance in the presence of both full state information as well as when entropic variables are unknown, confirming that the proposed approach exhibits superior accuracy and scalability without compromising on model expressivity.
(Joint with Kookjin Lee, Haksoo Lim, Noseong Park, and Nathaniel Trask.)
Variationally Consistent Hamiltonian Model Reduction Preprint
 Abstract: Though ubiquitous as first-principles models for conservative phenomena, Hamiltonian systems present numerous challenges for model reduction even in relatively simple, linear cases. Here, we present a method for the projection-based model reduction of canonical Hamiltonian systems that is variationally consistent for any choice of linear reduced basis: Hamiltonian models project to Hamiltonian models. Applicable in both intrusive and nonintrusive settings, the proposed method is energy-conserving and symplectic, with error provably decomposable into a data projection term and a term measuring deviation from canonical form. Examples from linear elasticity with realistic material parameters are used to demonstrate the advantages of a variationally consistent approach, highlighting the steady convergence exhibited by consistent models where previous methods reliant on inconsistent techniques or specially designed bases exhibit unacceptably large errors.
Abstract: Though ubiquitous as first-principles models for conservative phenomena, Hamiltonian systems present numerous challenges for model reduction even in relatively simple, linear cases. Here, we present a method for the projection-based model reduction of canonical Hamiltonian systems that is variationally consistent for any choice of linear reduced basis: Hamiltonian models project to Hamiltonian models. Applicable in both intrusive and nonintrusive settings, the proposed method is energy-conserving and symplectic, with error provably decomposable into a data projection term and a term measuring deviation from canonical form. Examples from linear elasticity with realistic material parameters are used to demonstrate the advantages of a variationally consistent approach, highlighting the steady convergence exhibited by consistent models where previous methods reliant on inconsistent techniques or specially designed bases exhibit unacceptably large errors.
(Joint with Irina Tezaur.)
Reversible and Irreversible Bracket-Based Dynamics for Deep Graph Neural Networks Preprint
 Abstract: Recent works have shown that physics-inspired architectures allow the training of deep graph neural networks (GNNs) without oversmoothing. The role of these physics is unclear, however, with successful examples of both reversible (e.g., Hamiltonian) and irreversible (e.g., diffusion) phenomena producing comparable results despite diametrically opposed mechanisms, and further complications arising due to empirical departures from mathematical theory. This work presents a series of novel GNN architectures based upon structure-preserving bracket-based dynamical systems, which are provably guaranteed to either conserve energy or generate positive dissipation with increasing depth. It is shown that the theoretically principled framework employed here allows for inherently explainable constructions, which contextualize departures from theory in current architectures and better elucidate the roles of reversibility and irreversibility in network performance
Abstract: Recent works have shown that physics-inspired architectures allow the training of deep graph neural networks (GNNs) without oversmoothing. The role of these physics is unclear, however, with successful examples of both reversible (e.g., Hamiltonian) and irreversible (e.g., diffusion) phenomena producing comparable results despite diametrically opposed mechanisms, and further complications arising due to empirical departures from mathematical theory. This work presents a series of novel GNN architectures based upon structure-preserving bracket-based dynamical systems, which are provably guaranteed to either conserve energy or generate positive dissipation with increasing depth. It is shown that the theoretically principled framework employed here allows for inherently explainable constructions, which contextualize departures from theory in current architectures and better elucidate the roles of reversibility and irreversibility in network performance
(Joint with Kookjin Lee and Nathaniel Trask.)
Canonical and Noncanonical Hamiltonian Operator Inference Preprint
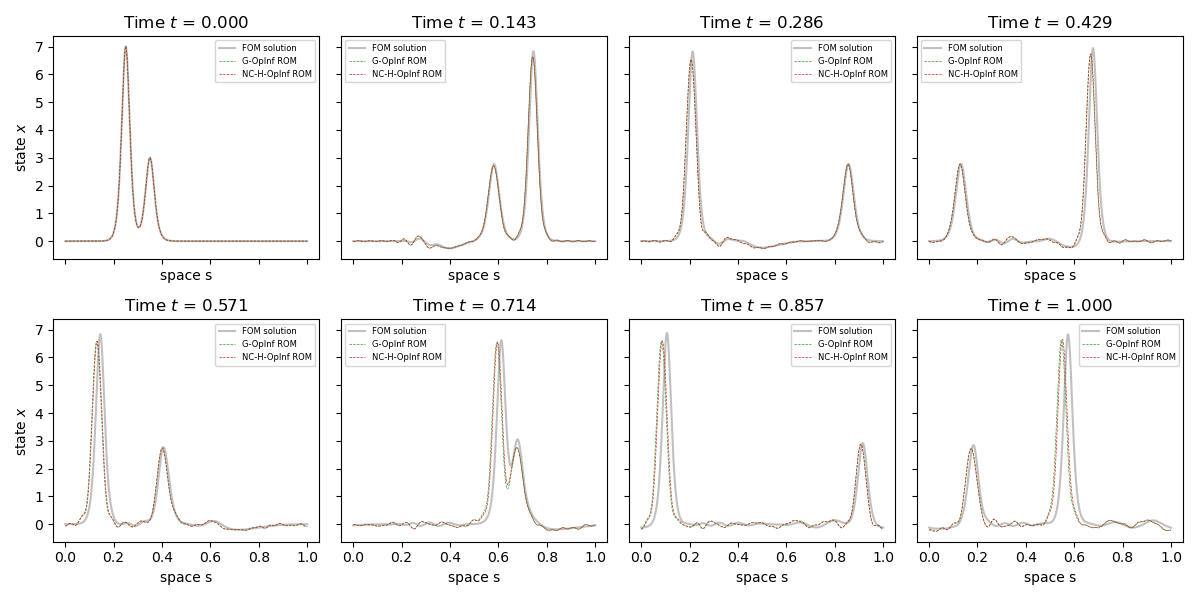 Abstract: A method for the nonintrusive and structure-preserving model reduction of canonical and noncanonical Hamiltonian systems is presented. Based on the idea of operator inference, this technique is provably convergent and reduces to a straightforward linear solve given snapshot data and gray-box knowledge of the system Hamiltonian. Examples involving several hyperbolic partial differential equations show that the proposed method yields reduced models which, in addition to being accurate and stable with respect to the addition of basis modes, preserve conserved quantities well outside the range of their training data.
Abstract: A method for the nonintrusive and structure-preserving model reduction of canonical and noncanonical Hamiltonian systems is presented. Based on the idea of operator inference, this technique is provably convergent and reduces to a straightforward linear solve given snapshot data and gray-box knowledge of the system Hamiltonian. Examples involving several hyperbolic partial differential equations show that the proposed method yields reduced models which, in addition to being accurate and stable with respect to the addition of basis modes, preserve conserved quantities well outside the range of their training data.
(Joint with Irina Tezaur.)
 Abstract: Uncertainties in an output of interest that depends on the solution of a complex system (e.g., of partial differential equations with random inputs) are often, if not nearly ubiquitously, determined in practice using Monte Carlo (MC) estimation. While simple to implement, MC estimation fails to provide reliable information about statistical quantities (such as the expected value of the output of interest) in application settings such as climate modeling for which obtaining a single realization of the output of interest is a costly endeavor. Specifically, the dilemma encountered is that many samples of the output of interest have to be collected in order to obtain an MC estimator having sufficient accuracy; so many, in fact, that the available computational budget is not large enough to effect the number of samples needed. To circumvent this dilemma, we consider using multifidelity Monte Carlo (MFMC) estimation which leverages the use of less costly and less accurate surrogate models (such as coarser grids, reduced-order models, simplified physics, interpolants, etc.) to achieve, for the same computational budget, higher accuracy compared to that obtained by an MC estimator or, looking at it another way, an MFMC estimator obtains the same accuracy as the MC estimator at lower computational cost. The key to the efficacy of MFMC estimation is the fact that most of the required computational budget is loaded onto the less costly surrogate models, so that very few samples are taken of the more expensive model of interest. We first provide a more detailed discussion about the need to consider an alternate to MC estimation for uncertainty quantification. Subsequently, we present a review, in an abstract setting, of the MFMC approach along with its application to three climate-related benchmark problems as a proof-of-concept exercise.
Abstract: Uncertainties in an output of interest that depends on the solution of a complex system (e.g., of partial differential equations with random inputs) are often, if not nearly ubiquitously, determined in practice using Monte Carlo (MC) estimation. While simple to implement, MC estimation fails to provide reliable information about statistical quantities (such as the expected value of the output of interest) in application settings such as climate modeling for which obtaining a single realization of the output of interest is a costly endeavor. Specifically, the dilemma encountered is that many samples of the output of interest have to be collected in order to obtain an MC estimator having sufficient accuracy; so many, in fact, that the available computational budget is not large enough to effect the number of samples needed. To circumvent this dilemma, we consider using multifidelity Monte Carlo (MFMC) estimation which leverages the use of less costly and less accurate surrogate models (such as coarser grids, reduced-order models, simplified physics, interpolants, etc.) to achieve, for the same computational budget, higher accuracy compared to that obtained by an MC estimator or, looking at it another way, an MFMC estimator obtains the same accuracy as the MC estimator at lower computational cost. The key to the efficacy of MFMC estimation is the fact that most of the required computational budget is loaded onto the less costly surrogate models, so that very few samples are taken of the more expensive model of interest. We first provide a more detailed discussion about the need to consider an alternate to MC estimation for uncertainty quantification. Subsequently, we present a review, in an abstract setting, of the MFMC approach along with its application to three climate-related benchmark problems as a proof-of-concept exercise.
(Joint with Max Gunzburger, Lili Ju, Rihui Lan, and Zhu Wang.)
A Multifidelity Monte Carlo Method for Realistic Computational Budgets Preprint
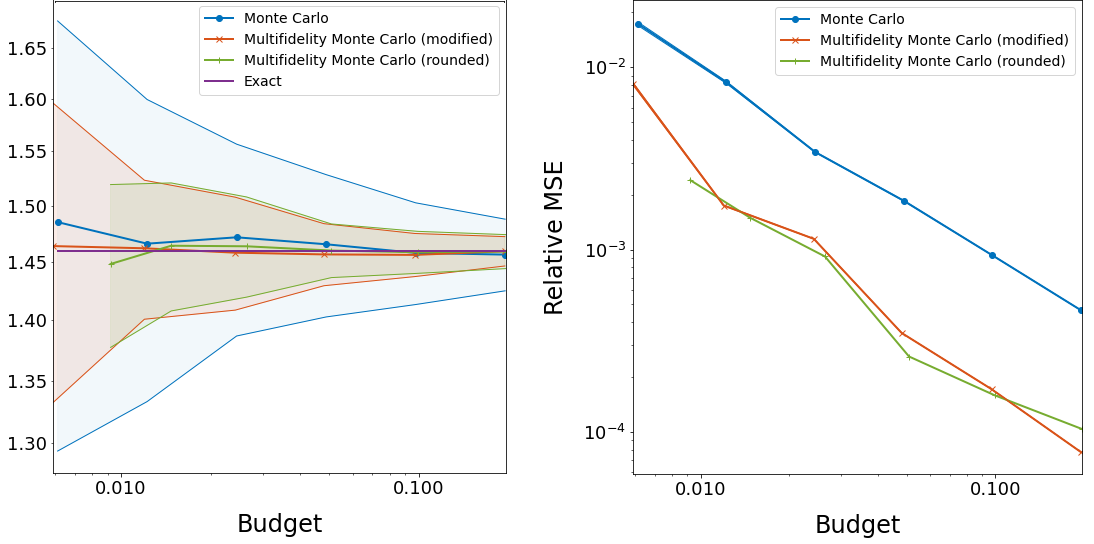 Abstract: A method for the multifidelity Monte Carlo (MFMC) estimation of statistical quantities is proposed which is applicable to computational budgets of any size. Based on a sequence of optimization problems each with a globally minimizing closed-form solution, this method extends the usability of a well known MFMC algorithm, recovering it when the computational budget is large enough. Theoretical results verify that the proposed approach is at least as optimal as its namesake and retains the benefits of multifidelity estimation with minimal assumptions on the budget or amount of available data, providing a notable reduction in variance over simple Monte Carlo estimation.
Abstract: A method for the multifidelity Monte Carlo (MFMC) estimation of statistical quantities is proposed which is applicable to computational budgets of any size. Based on a sequence of optimization problems each with a globally minimizing closed-form solution, this method extends the usability of a well known MFMC algorithm, recovering it when the computational budget is large enough. Theoretical results verify that the proposed approach is at least as optimal as its namesake and retains the benefits of multifidelity estimation with minimal assumptions on the budget or amount of available data, providing a notable reduction in variance over simple Monte Carlo estimation.
(Joint with Max Gunzburger, Lili Ju, and Zhu Wang.)
Energetically Consistent Model Reduction for Metriplectic Systems Preprint
 Abstract: The metriplectic formalism is useful for describing complete dynamical systems which conserve energy and produce entropy. This creates challenges for model reduction, as the elimination of high-frequency information will generally not preserve the metriplectic structure which governs long-term stability of the system. Based on proper orthogonal decomposition, a provably convergent metriplectic reduced-order model is formulated which is guaranteed to maintain the algebraic structure necessary for energy conservation and entropy formation. Numerical results on benchmark problems show that the proposed method is remarkably stable, leading to improved accuracy over long time scales at a moderate increase in cost over naive methods.
Abstract: The metriplectic formalism is useful for describing complete dynamical systems which conserve energy and produce entropy. This creates challenges for model reduction, as the elimination of high-frequency information will generally not preserve the metriplectic structure which governs long-term stability of the system. Based on proper orthogonal decomposition, a provably convergent metriplectic reduced-order model is formulated which is guaranteed to maintain the algebraic structure necessary for energy conservation and entropy formation. Numerical results on benchmark problems show that the proposed method is remarkably stable, leading to improved accuracy over long time scales at a moderate increase in cost over naive methods.
(Joint with Max Gunzburger, Lili Ju, and Zhu Wang.)
Comparing Neural Architectures for Reduced-Order Modeling Preprint Read More
 Abstract: The popularity of deep convolutional autoencoders (CAEs) has engendered new and effective reduced-order models (ROMs) for the simulation of large-scale dynamical systems. Despite this, it is still unknown whether deep CAEs provide superior performance over established linear techniques or other network-based methods in all modeling scenarios. To elucidate this, the effect of autoencoder architecture on its associated ROM is studied through the comparison of deep CAEs against two alternatives: a simple fully connected autoencoder, and a novel graph convolutional autoencoder. Through benchmark experiments, it is shown that the superior autoencoder architecture for a given ROM application is highly dependent on the size of the latent space and the structure of the snapshot data, with the proposed architecture demonstrating benefits on data with irregular connectivity when the latent space is sufficiently large.
Abstract: The popularity of deep convolutional autoencoders (CAEs) has engendered new and effective reduced-order models (ROMs) for the simulation of large-scale dynamical systems. Despite this, it is still unknown whether deep CAEs provide superior performance over established linear techniques or other network-based methods in all modeling scenarios. To elucidate this, the effect of autoencoder architecture on its associated ROM is studied through the comparison of deep CAEs against two alternatives: a simple fully connected autoencoder, and a novel graph convolutional autoencoder. Through benchmark experiments, it is shown that the superior autoencoder architecture for a given ROM application is highly dependent on the size of the latent space and the structure of the snapshot data, with the proposed architecture demonstrating benefits on data with irregular connectivity when the latent space is sufficiently large.
(Joint with Max Gunzburger, Lili Ju, and Zhu Wang.)
Learning the Structure of Level Sets from Sparse Data Preprint Read More
 Abstract: A dimension reduction method based on the ``Nonlinear Level set Learning’’ (NLL) approach is presented for the pointwise prediction of functions which have been sparsely sampled. Leveraging geometric information provided by the Implicit Function Theorem, the proposed algorithm effectively reduces the input dimension to the theoretical lower bound with minor accuracy loss, providing a one-dimensional representation of the function which can be used for regression and sensitivity analysis. Experiments and applications are presented which compare this modified NLL with the original NLL and the Active Subspaces (AS) method. While accommodating sparse input data, the proposed algorithm is shown to train quickly and provide a much more accurate and informative reduction than either AS or the original NLL on two example functions with high-dimensional domains, as well as two state-dependent quantities depending on the solutions to parametric differential equations.
Abstract: A dimension reduction method based on the ``Nonlinear Level set Learning’’ (NLL) approach is presented for the pointwise prediction of functions which have been sparsely sampled. Leveraging geometric information provided by the Implicit Function Theorem, the proposed algorithm effectively reduces the input dimension to the theoretical lower bound with minor accuracy loss, providing a one-dimensional representation of the function which can be used for regression and sensitivity analysis. Experiments and applications are presented which compare this modified NLL with the original NLL and the Active Subspaces (AS) method. While accommodating sparse input data, the proposed algorithm is shown to train quickly and provide a much more accurate and informative reduction than either AS or the original NLL on two example functions with high-dimensional domains, as well as two state-dependent quantities depending on the solutions to parametric differential equations.
(Joint with Max Gunzburger, Lili Ju, Yuankai Teng, and Zhu Wang.)
Pseudo-Reversible Neural Networks Preprint
 Abstract: Due to the curse of dimensionality and limitations on training data, approximating high-dimensional functions is a very challenging task even for powerful deep neural networks. Inspired by the Nonlinear Level set Learning (NLL) method that uses the reversible residual network (RevNet), in this paper we propose a new method for function approximation called Dimension Reduction via Learning Level Sets (DRiLLS). Our method contains two major components: one is the pseudo-reversible neural network (PRNN) module that effectively transforms high-dimensional input variables to low-dimensional active variables, and the other is the synthesized regression module for approximating function values based on the transformed data in the low-dimensional space. Extensive experimental results demonstrate that DRiLLS outperforms both the NLL and Active Subspace methods, especially when the target function possesses critical points in the interior of its input domain.
Abstract: Due to the curse of dimensionality and limitations on training data, approximating high-dimensional functions is a very challenging task even for powerful deep neural networks. Inspired by the Nonlinear Level set Learning (NLL) method that uses the reversible residual network (RevNet), in this paper we propose a new method for function approximation called Dimension Reduction via Learning Level Sets (DRiLLS). Our method contains two major components: one is the pseudo-reversible neural network (PRNN) module that effectively transforms high-dimensional input variables to low-dimensional active variables, and the other is the synthesized regression module for approximating function values based on the transformed data in the low-dimensional space. Extensive experimental results demonstrate that DRiLLS outperforms both the NLL and Active Subspace methods, especially when the target function possesses critical points in the interior of its input domain.
(Joint with Lili Ju, Yuankai Teng, Zhu Wang, and Guannan Zhang.)
Active Manifolds: Geometric Data Analysis for Dimension Reduction Here Read More.
 Abstract: We present an approach to analyze \(C^1(\mathbb{R}^m)\) functions that addresses limitations present in the Active Subspaces (AS) method of Constantine et al. Under appropriate hypotheses, our Active Manifolds (AM) method identifies a 1-D curve in the domain (the active manifold) on which nearly all values of the unknown function are attained, and which can be exploited for approximation or analysis, especially when \(m\) is large (high-dimensional input space). We provide theorems justifying our AM technique and an algorithm permitting functional approximation and sensitivity analysis. Using accessible, low-dimensional functions as initial examples, we show AM reduces approximation error by an order of magnitude compared to AS, at the expense of more computation. Following this, we revisit the sensitivity analysis by Glaws et al. who apply AS to analyze a magnetohydrodynamic power generator model, and compare the performance of AM on the same data. Our analysis provides detailed information not captured by AS, exhibiting the influence of each parameter individually along an active manifold. Overall, AM represents a novel technique for analyzing functional models with benefits including: reducing \(m\)-dimensional analysis to a 1-D analogue, permitting more accurate regression than AS (at more computational expense), enabling more informative sensitivity analysis, and granting accessible visualizations (2-D plots) of parameter sensitivity along the AM.
Abstract: We present an approach to analyze \(C^1(\mathbb{R}^m)\) functions that addresses limitations present in the Active Subspaces (AS) method of Constantine et al. Under appropriate hypotheses, our Active Manifolds (AM) method identifies a 1-D curve in the domain (the active manifold) on which nearly all values of the unknown function are attained, and which can be exploited for approximation or analysis, especially when \(m\) is large (high-dimensional input space). We provide theorems justifying our AM technique and an algorithm permitting functional approximation and sensitivity analysis. Using accessible, low-dimensional functions as initial examples, we show AM reduces approximation error by an order of magnitude compared to AS, at the expense of more computation. Following this, we revisit the sensitivity analysis by Glaws et al. who apply AS to analyze a magnetohydrodynamic power generator model, and compare the performance of AM on the same data. Our analysis provides detailed information not captured by AS, exhibiting the influence of each parameter individually along an active manifold. Overall, AM represents a novel technique for analyzing functional models with benefits including: reducing \(m\)-dimensional analysis to a 1-D analogue, permitting more accurate regression than AS (at more computational expense), enabling more informative sensitivity analysis, and granting accessible visualizations (2-D plots) of parameter sensitivity along the AM.
(Joint with Robert Bridges, Christopher Felder, and Miki Verma.)
Rigidity Results for Immersed Submanifolds
 Many practical problems involving shape deformation can be understood in the context of “allowable” mappings between Riemannan spaces. When these mappings are constrained by natural geometric conditions on e.g. curvature, their existence is governed by overdetermined PDEs which are difficult to approach using classical analytic techniques. These projects establish characterization results in my preferred style for certain classes of mappings which I have encountered in applications.
Many practical problems involving shape deformation can be understood in the context of “allowable” mappings between Riemannan spaces. When these mappings are constrained by natural geometric conditions on e.g. curvature, their existence is governed by overdetermined PDEs which are difficult to approach using classical analytic techniques. These projects establish characterization results in my preferred style for certain classes of mappings which I have encountered in applications.
(Hopf torus courtesy of Álvaro Pámpano.)
Projects
Planar Immersions with Prescribed Curl and Jacobian Determinant are Unique Preprint
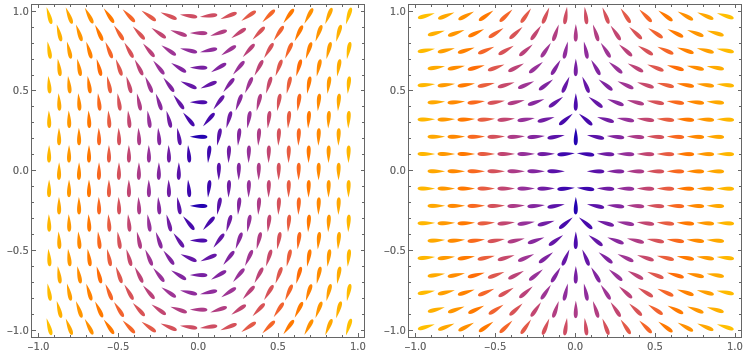 Abstract: We prove that immersions of planar domains are uniquely specified by their Jacobian determinant, curl function, and boundary values. This settles the two-dimensional version of an outstanding conjecture related to a particular grid generation method in computer graphics.
Abstract: We prove that immersions of planar domains are uniquely specified by their Jacobian determinant, curl function, and boundary values. This settles the two-dimensional version of an outstanding conjecture related to a particular grid generation method in computer graphics.
Parallel Codazzi Tensors with Submanifold Applications Preprint
 Abstract: A decomposition theorem is established for a class of closed Riemannian submanifolds immersed in a space form of constant sectional curvature. In particular, it is shown that if \(M\) has nonnegative sectional curvature and admits a Codazzi tensor with “parallel mean curvature”, then \(M\) is locally isometric to a direct product of irreducible factors determined by the spectrum of that tensor. This decomposition is global when \(M\) is simply connected, and generalizes what is known for immersed submanifolds with parallel mean curvature vector.
Abstract: A decomposition theorem is established for a class of closed Riemannian submanifolds immersed in a space form of constant sectional curvature. In particular, it is shown that if \(M\) has nonnegative sectional curvature and admits a Codazzi tensor with “parallel mean curvature”, then \(M\) is locally isometric to a direct product of irreducible factors determined by the spectrum of that tensor. This decomposition is global when \(M\) is simply connected, and generalizes what is known for immersed submanifolds with parallel mean curvature vector.
Quaternionic Surface Theory for Graphics and Meshing
 Just as classical complex analysis facilitates study of the conformal geometry of planar domains, the rich algebraic structure of the quaternions enables a useful framework for describing the conformal geometry of surfaces in Euclidean space. These projects develop and use quaternionic surface theory for graphics and meshing applications.
Just as classical complex analysis facilitates study of the conformal geometry of planar domains, the rich algebraic structure of the quaternions enables a useful framework for describing the conformal geometry of surfaces in Euclidean space. These projects develop and use quaternionic surface theory for graphics and meshing applications.
Projects
Quasiconformal Mappings with Surface Domains Preprint
 Abstract: Quasiconformal mappings from surfaces immersed in Euclidean space are discussed for the purposes of computing dilatation-optimal surface meshes with prescribed connectivity and Dirichlet boundary data. In particular, a quaternionic formulation of quasiconformality is proposed which leads to a linear algorithm for computing least-squares quasiconformal maps from surfaces given as extrinsic mesh data. This facilitates an iterative procedure which computes optimal quasiconformal mappings with optional constraints on surface area and extrinsic geometry. Based on the established Quasiconformal Iteration method, the proposed algorithm produces high quality surface mappings which correctly capture boundary information while eliminating undesirable folds which appear during least-squares conformal mapping procedures.
Abstract: Quasiconformal mappings from surfaces immersed in Euclidean space are discussed for the purposes of computing dilatation-optimal surface meshes with prescribed connectivity and Dirichlet boundary data. In particular, a quaternionic formulation of quasiconformality is proposed which leads to a linear algorithm for computing least-squares quasiconformal maps from surfaces given as extrinsic mesh data. This facilitates an iterative procedure which computes optimal quasiconformal mappings with optional constraints on surface area and extrinsic geometry. Based on the established Quasiconformal Iteration method, the proposed algorithm produces high quality surface mappings which correctly capture boundary information while eliminating undesirable folds which appear during least-squares conformal mapping procedures.
(Joint with Eugenio Aulisa.)
Modeling the p-Willmore Flow of Surfaces Here Read More
 Abstract: The unsigned p-Willmore functional generalizes important geometric functionals which measure the area and Willmore energy of immersed surfaces. Presently, techniques of Dziuk are adapted to compute the first variation of this functional as a weak-form system of equations, which are subsequently used to develop a model for the p-Willmore flow of closed surfaces in \(\mathbb{R}^3\). This model is amenable to constraints on surface area and enclosed volume, and is shown to decrease the p-Willmore energy monotonically. In addition, a penalty-based regularization procedure is formulated to prevent artificial mesh degeneration along the flow; inspired by a conformality condition derived by Kamberov et al., this procedure encourages angle-preservation in a closed and oriented surface immersion as it evolves. Following this, a finite-element discretization of both procedures is discussed, an algorithm for running the flow is given, and an application to mesh editing is presented.
Abstract: The unsigned p-Willmore functional generalizes important geometric functionals which measure the area and Willmore energy of immersed surfaces. Presently, techniques of Dziuk are adapted to compute the first variation of this functional as a weak-form system of equations, which are subsequently used to develop a model for the p-Willmore flow of closed surfaces in \(\mathbb{R}^3\). This model is amenable to constraints on surface area and enclosed volume, and is shown to decrease the p-Willmore energy monotonically. In addition, a penalty-based regularization procedure is formulated to prevent artificial mesh degeneration along the flow; inspired by a conformality condition derived by Kamberov et al., this procedure encourages angle-preservation in a closed and oriented surface immersion as it evolves. Following this, a finite-element discretization of both procedures is discussed, an algorithm for running the flow is given, and an application to mesh editing is presented.
(Joint with Eugenio Aulisa.)
Curvature Functionals and p-Willmore Energy
 Functionals involving surface curvature are widely used as models for elastic phenomena, and their critical points are frequently representative of physically relevant structures such as biomembranes or material interfaces. These projects involve a variational characterization of curvature functionals and their critical surfaces, both from a general perspective and in multiple specific cases of interest.
Functionals involving surface curvature are widely used as models for elastic phenomena, and their critical points are frequently representative of physically relevant structures such as biomembranes or material interfaces. These projects involve a variational characterization of curvature functionals and their critical surfaces, both from a general perspective and in multiple specific cases of interest.
Projects
Instability of Closed \(p\)-Elastic Curves in \(\mathcal{S}^2\) Preprint
 Abstract: For \(p \in \mathbb{R}\), we show that non-circular closed p-elastic curves in \(\mathbb{S}^2\) exist only when \(p=2\), in which case they are classical elastic curves, or when \(p\in(0,1)\). In the latter case, we prove that for every pair of relatively prime natural numbers \(n\) and \(m\) satisfying \(m<2n<2\sqrt{m}\), there exists a closed spherical \(p\)-elastic curve with non-constant curvature which winds around a pole \(n\) times and closes up in m periods of its curvature. Further, we show that all closed spherical \(p\)-elastic curves for \(p\in(0,1)\) are unstable as critical points of the p-elastic energy.
Abstract: For \(p \in \mathbb{R}\), we show that non-circular closed p-elastic curves in \(\mathbb{S}^2\) exist only when \(p=2\), in which case they are classical elastic curves, or when \(p\in(0,1)\). In the latter case, we prove that for every pair of relatively prime natural numbers \(n\) and \(m\) satisfying \(m<2n<2\sqrt{m}\), there exists a closed spherical \(p\)-elastic curve with non-constant curvature which winds around a pole \(n\) times and closes up in m periods of its curvature. Further, we show that all closed spherical \(p\)-elastic curves for \(p\in(0,1)\) are unstable as critical points of the p-elastic energy.
(Joint with Magdalena Toda and Álvaro Pámpano.)
On p-Willmore Disks with Boundary Energies Preprint
 Abstract: We consider an energy functional on surface immersions which includes contributions from both boundary and interior. Inspired by physical examples, the boundary is modeled as the center line of a generalized Kirchhoff elastic rod, while the interior term is arbitrarily dependent on the mean curvature and linearly dependent on the Gaussian curvature. We study equilibrium configurations for this energy in general among topological disks, as well as specifically for the class of examples known as p-Willmore energies.
Abstract: We consider an energy functional on surface immersions which includes contributions from both boundary and interior. Inspired by physical examples, the boundary is modeled as the center line of a generalized Kirchhoff elastic rod, while the interior term is arbitrarily dependent on the mean curvature and linearly dependent on the Gaussian curvature. We study equilibrium configurations for this energy in general among topological disks, as well as specifically for the class of examples known as p-Willmore energies.
(Joint with Magdalena Toda and Álvaro Pámpano.)
Regarding the Euler-Plateau Problem with Elastic Modulus Preprint
 Abstract: We study equilibrium configurations for the Euler-Plateau energy with elastic modulus, which couples an energy functional of Euler-Plateau type with a total curvature term often present in models for the free energy of biomembranes. It is shown that the potential minimizers of this energy are highly dependent on the choice of physical rigidity parameters, and that the area of critical surfaces can be computed entirely from their boundary data. When the elastic modulus does not vanish, it is shown that axially symmetric critical immersions and critical immersions of disk type are necessarily planar domains bounded by area-constrained elasticae. The cases of topological genus zero with multiple boundary components and unrestricted genus with control on the geodesic torsion are also discussed, and sufficient conditions are given which establish the same conclusion in these cases.
Abstract: We study equilibrium configurations for the Euler-Plateau energy with elastic modulus, which couples an energy functional of Euler-Plateau type with a total curvature term often present in models for the free energy of biomembranes. It is shown that the potential minimizers of this energy are highly dependent on the choice of physical rigidity parameters, and that the area of critical surfaces can be computed entirely from their boundary data. When the elastic modulus does not vanish, it is shown that axially symmetric critical immersions and critical immersions of disk type are necessarily planar domains bounded by area-constrained elasticae. The cases of topological genus zero with multiple boundary components and unrestricted genus with control on the geodesic torsion are also discussed, and sufficient conditions are given which establish the same conclusion in these cases.
(Joint with Magdalena Toda and Álvaro Pámpano.)
Stationary Surfaces with Boundaries Preprint
 Abstract: This article investigates stationary surfaces with boundaries, which arise as the critical points of functionals dependent on curvature. Precisely, a generalized “bending energy” functional \(\mathcal{W}\) is considered which involves a Lagrangian that is symmetric in the principal curvatures. The first variation of \(\mathcal{W}\) is computed, and a stress tensor is extracted whose divergence quantifies deviation from \(\mathcal{W}\)-criticality. Boundary-value problems are then examined, and a characterization of free-boundary \(\mathcal{W}\)-surfaces with rotational symmetry is given for scaling-invariant \(\mathcal{W}\)-functionals. In case the functional is not scaling-invariant, certain boundary-to-interior consequences are discussed. Finally, some applications to the conformal Willmore energy and the p-Willmore energy of surfaces are presented.
Abstract: This article investigates stationary surfaces with boundaries, which arise as the critical points of functionals dependent on curvature. Precisely, a generalized “bending energy” functional \(\mathcal{W}\) is considered which involves a Lagrangian that is symmetric in the principal curvatures. The first variation of \(\mathcal{W}\) is computed, and a stress tensor is extracted whose divergence quantifies deviation from \(\mathcal{W}\)-criticality. Boundary-value problems are then examined, and a characterization of free-boundary \(\mathcal{W}\)-surfaces with rotational symmetry is given for scaling-invariant \(\mathcal{W}\)-functionals. In case the functional is not scaling-invariant, certain boundary-to-interior consequences are discussed. Finally, some applications to the conformal Willmore energy and the p-Willmore energy of surfaces are presented.
(Joint with Magdalena Toda and Hung Tran.)
 Abstract: Functionals involving surface curvature are important across a range of scientific disciplines, and their extrema are representative of physically meaningful objects such as atomic lattices and biomembranes. Inspired in particular by the relationship of the Willmore energy to lipid bilayers, we consider a general functional depending on a surface and a symmetric combination of its principal curvatures, provided the surface is immersed in a 3-D space form. We compute the first and second variations of this functional, leading to expressions given entirely in terms of the surface fundamental forms. We then apply the stability criteria afforded by our calculations to a generalization of the Willmore functional, proving a result regarding the stability of spheres.
Abstract: Functionals involving surface curvature are important across a range of scientific disciplines, and their extrema are representative of physically meaningful objects such as atomic lattices and biomembranes. Inspired in particular by the relationship of the Willmore energy to lipid bilayers, we consider a general functional depending on a surface and a symmetric combination of its principal curvatures, provided the surface is immersed in a 3-D space form. We compute the first and second variations of this functional, leading to expressions given entirely in terms of the surface fundamental forms. We then apply the stability criteria afforded by our calculations to a generalization of the Willmore functional, proving a result regarding the stability of spheres.
(Joint with Magdalena Toda and Hung Tran.)
Curvature Functionals and p-Willmore Energy Here Read More
 My PhD thesis, which investigates many aspects of general curvature functionals in the abstract, and applies some of them to the particular case of the p-Willmore energy.
My PhD thesis, which investigates many aspects of general curvature functionals in the abstract, and applies some of them to the particular case of the p-Willmore energy.
Abstract: Functionals involving surface curvature are frequently encountered when modeling the behavior of important biological structures such as lipid membranes. To better understand these objects, we consider a general functional on surface immersions which is dependent on the surface mean and Gauss curvatures. Variations of this functional are presented, and stability criteria are given in terms of basic geometric invariants coming from the surface fundamental forms. These results are then applied to a particular curvature functional which generalizes the Willmore energy, and a nonexistence result is presented. A constrained minimization problem is then considered, leading to a stability result involving round spheres. Further study is done on a generalization of the Willmore flow of surfaces in $\mathbb{R}^3$ – a geometric tool known for its aesthetic beauty. In particular, two finite-element formulations of this problem are presented: one which is applicable to surfaces presented graphically, and the other which models closed immersed (possibly self-intersecting) surfaces and is amenable to constraints on surface area and enclosed volume. It is shown in both cases that the energy decreases along the flow. Moreover, stability and consistency results are obtained in the closed surface model, and examples of the implementation are discussed. Inspired by conformal geometry, a post-processing procedure is also presented, which ensures that a given surface mesh remains nearly conformal along the Willmore flow despite its initial regularity. This abolishes the mesh degeneration that usually accompanies position-based surface flows, and leads to a robust model that can accommodate variable time steps as well as surface genera.



 Due to their high computational cost, scientific studies based on large-scale simulation frequently operate at a data deficit which creates problems inverse to the issues with “big data”. Particularly, there is a need for efficient function approximation and model reduction strategies which can serve as cheap and reliable surrogates for the high-fidelity models used in practical applications. These projects develop such technology using invariances and other structural considerations as a starting point, allowing for informed surrogates with beneficial behavior.
Due to their high computational cost, scientific studies based on large-scale simulation frequently operate at a data deficit which creates problems inverse to the issues with “big data”. Particularly, there is a need for efficient function approximation and model reduction strategies which can serve as cheap and reliable surrogates for the high-fidelity models used in practical applications. These projects develop such technology using invariances and other structural considerations as a starting point, allowing for informed surrogates with beneficial behavior.



 Abstract: A method for the nonintrusive and structure-preserving model reduction of canonical and noncanonical Hamiltonian systems is presented. Based on the idea of operator inference, this technique is provably convergent and reduces to a straightforward linear solve given snapshot data and gray-box knowledge of the system Hamiltonian. Examples involving several hyperbolic partial differential equations show that the proposed method yields reduced models which, in addition to being accurate and stable with respect to the addition of basis modes, preserve conserved quantities well outside the range of their training data.
Abstract: A method for the nonintrusive and structure-preserving model reduction of canonical and noncanonical Hamiltonian systems is presented. Based on the idea of operator inference, this technique is provably convergent and reduces to a straightforward linear solve given snapshot data and gray-box knowledge of the system Hamiltonian. Examples involving several hyperbolic partial differential equations show that the proposed method yields reduced models which, in addition to being accurate and stable with respect to the addition of basis modes, preserve conserved quantities well outside the range of their training data. 
 Abstract: A method for the multifidelity Monte Carlo (MFMC) estimation of statistical quantities is proposed which is applicable to computational budgets of any size. Based on a sequence of optimization problems each with a globally minimizing closed-form solution, this method extends the usability of a well known MFMC algorithm, recovering it when the computational budget is large enough. Theoretical results verify that the proposed approach is at least as optimal as its namesake and retains the benefits of multifidelity estimation with minimal assumptions on the budget or amount of available data, providing a notable reduction in variance over simple Monte Carlo estimation.
Abstract: A method for the multifidelity Monte Carlo (MFMC) estimation of statistical quantities is proposed which is applicable to computational budgets of any size. Based on a sequence of optimization problems each with a globally minimizing closed-form solution, this method extends the usability of a well known MFMC algorithm, recovering it when the computational budget is large enough. Theoretical results verify that the proposed approach is at least as optimal as its namesake and retains the benefits of multifidelity estimation with minimal assumptions on the budget or amount of available data, providing a notable reduction in variance over simple Monte Carlo estimation. 




 Many practical problems involving shape deformation can be understood in the context of “allowable” mappings between Riemannan spaces. When these mappings are constrained by natural geometric conditions on e.g. curvature, their existence is governed by overdetermined PDEs which are difficult to approach using classical analytic techniques. These projects establish characterization results in my preferred style for certain classes of mappings which I have encountered in applications.
Many practical problems involving shape deformation can be understood in the context of “allowable” mappings between Riemannan spaces. When these mappings are constrained by natural geometric conditions on e.g. curvature, their existence is governed by overdetermined PDEs which are difficult to approach using classical analytic techniques. These projects establish characterization results in my preferred style for certain classes of mappings which I have encountered in applications. Abstract: We prove that immersions of planar domains are uniquely specified by their Jacobian determinant, curl function, and boundary values. This settles the two-dimensional version of an outstanding conjecture related to a particular grid generation method in computer graphics.
Abstract: We prove that immersions of planar domains are uniquely specified by their Jacobian determinant, curl function, and boundary values. This settles the two-dimensional version of an outstanding conjecture related to a particular grid generation method in computer graphics. 
 Just as classical complex analysis facilitates study of the conformal geometry of planar domains, the rich algebraic structure of the quaternions enables a useful framework for describing the conformal geometry of surfaces in Euclidean space. These projects develop and use quaternionic surface theory for graphics and meshing applications.
Just as classical complex analysis facilitates study of the conformal geometry of planar domains, the rich algebraic structure of the quaternions enables a useful framework for describing the conformal geometry of surfaces in Euclidean space. These projects develop and use quaternionic surface theory for graphics and meshing applications. Abstract: Quasiconformal mappings from surfaces immersed in Euclidean space are discussed for the purposes of computing dilatation-optimal surface meshes with prescribed connectivity and Dirichlet boundary data. In particular, a quaternionic formulation of quasiconformality is proposed which leads to a linear algorithm for computing least-squares quasiconformal maps from surfaces given as extrinsic mesh data. This facilitates an iterative procedure which computes optimal quasiconformal mappings with optional constraints on surface area and extrinsic geometry. Based on the established Quasiconformal Iteration method, the proposed algorithm produces high quality surface mappings which correctly capture boundary information while eliminating undesirable folds which appear during least-squares conformal mapping procedures.
Abstract: Quasiconformal mappings from surfaces immersed in Euclidean space are discussed for the purposes of computing dilatation-optimal surface meshes with prescribed connectivity and Dirichlet boundary data. In particular, a quaternionic formulation of quasiconformality is proposed which leads to a linear algorithm for computing least-squares quasiconformal maps from surfaces given as extrinsic mesh data. This facilitates an iterative procedure which computes optimal quasiconformal mappings with optional constraints on surface area and extrinsic geometry. Based on the established Quasiconformal Iteration method, the proposed algorithm produces high quality surface mappings which correctly capture boundary information while eliminating undesirable folds which appear during least-squares conformal mapping procedures. 






 My PhD thesis, which investigates many aspects of general curvature functionals in the abstract, and applies some of them to the particular case of the p-Willmore energy.
My PhD thesis, which investigates many aspects of general curvature functionals in the abstract, and applies some of them to the particular case of the p-Willmore energy. 
