Quasiconformal Mappings for Surface Mesh Optimization

\[\newcommand{\nn}[1]{\left|#1\right|} \newcommand{\mm}[1]{#1^{-}} \newcommand{\pp}[1]{#1^{+}} \newcommand{\bb}[1]{\mathbf{#1}} \newcommand{\zbar}{\bar{z}} \newcommand{\wbar}{\bar{w}} \newcommand{\bmp}{\boldsymbol{\partial}} \newcommand{\ImH}{\mathrm{Im}\,\mathbb{H}} \newcommand{\vp}{\varphi} \newcommand{\argg}{\mathrm{arg}\,}\]

image-center

Recall that a quasiconformal map $f:M \to P$ between Riemann surfaces is an orientation-preserving homeomorphism with bounded conformality distortion. In a local conformal coordinate $z:U \to M$ such that $g=\sigma\nn{dz}^2$ for some positive function $\sigma:U \to \mathbb{R}$, quasiconformality implies the Beltrami equation,

\[\bb{f}_{\zbar} = \mu\,\bb{f}_z,\]

where $\bb{f}_z = \partial_z f$ (resp. $\bb{f}_{\zbar} = \partial_{\zbar} f$) are the partial derivatives of the mapping $f$ and $\mu:U \to \mathbb{C}$, is the locally defined Beltrami coefficient. Geometrically, the Beltrami equation implies that quasiconformal maps take small circles on the source space to small ellipses of bounded eccentricity on the target.

image-center

In this work, we apply quaternionic surface theory to form a global analogue of the local Beltrami equation, which enables a new algorithm for computing quasiconformal maps from Riemann surfaces into $\mathbb{R}^3$. In particular, recall that $f: M \to \mathbb{R}^3$ is said to be conformal provided it maps oriented orthogonal bases of $TM$ to oriented orthogonal bases of $df(TM)$, i.e. if and only if

\[\ast df = N\, df,\]

where $\ast df = df \circ J$ is the negative Hodge star operator and $N$ is the Gauss map of the immersion $f$. This gives a splitting of differential one-forms on $TM$ into conformal and anticonformal parts, enabling the coordinate-free Beltrami equation

\[\mm{df} = \pp{df} \circ \mu,\]

where $\mu: TM \to TM$ is a measurable complex-antilinear mapping and

\[df^{+} = \frac{1}{2}\left(df - N \ast df \right), \qquad df^{-} = \frac{1}{2}\left(df + N \ast df \right).\]

For explicit computation, note that $\mu$ has the dual interpretation as a normal valued quaternionic function $\mu = a + bN$ at each point, so that we can write

\[\mm{df} = \mu\,\pp{df},\]

which looks very much like the classical Beltrami equation. Using this, we develop an algorithm for computing dilatation-optimal quasiconformal mappings (i.e. Teichmüller maps) based on the Quasiconformal Iteration of Lui et al. (2012). More precisely, the idea of our algorithm is to minimize the quasiconformal distortion

\[\mathcal{QC}_\mu(f) = \int_M \nn{\mm{df} - \mu\,\pp{df}}^2 dS_g,\]

through the alternative minimization of $f$ and $\mu$. At a high level, the algorithm is

Compute $f_k:M\to\mathbb{R}^3$ given $\mu_k$.
Compute $\nu_{k+1}$ given $f_k$.
Post-process $\nu_{k+1}$ to bring it closer to \tm form, generating $\xi_{k+1}$.
Minimize $\mathcal{QC}_{\mu}(f_k)$ on the line between $\mu_k$ and $\xi_{k+1}$, generating $\mu_{k+1}$.

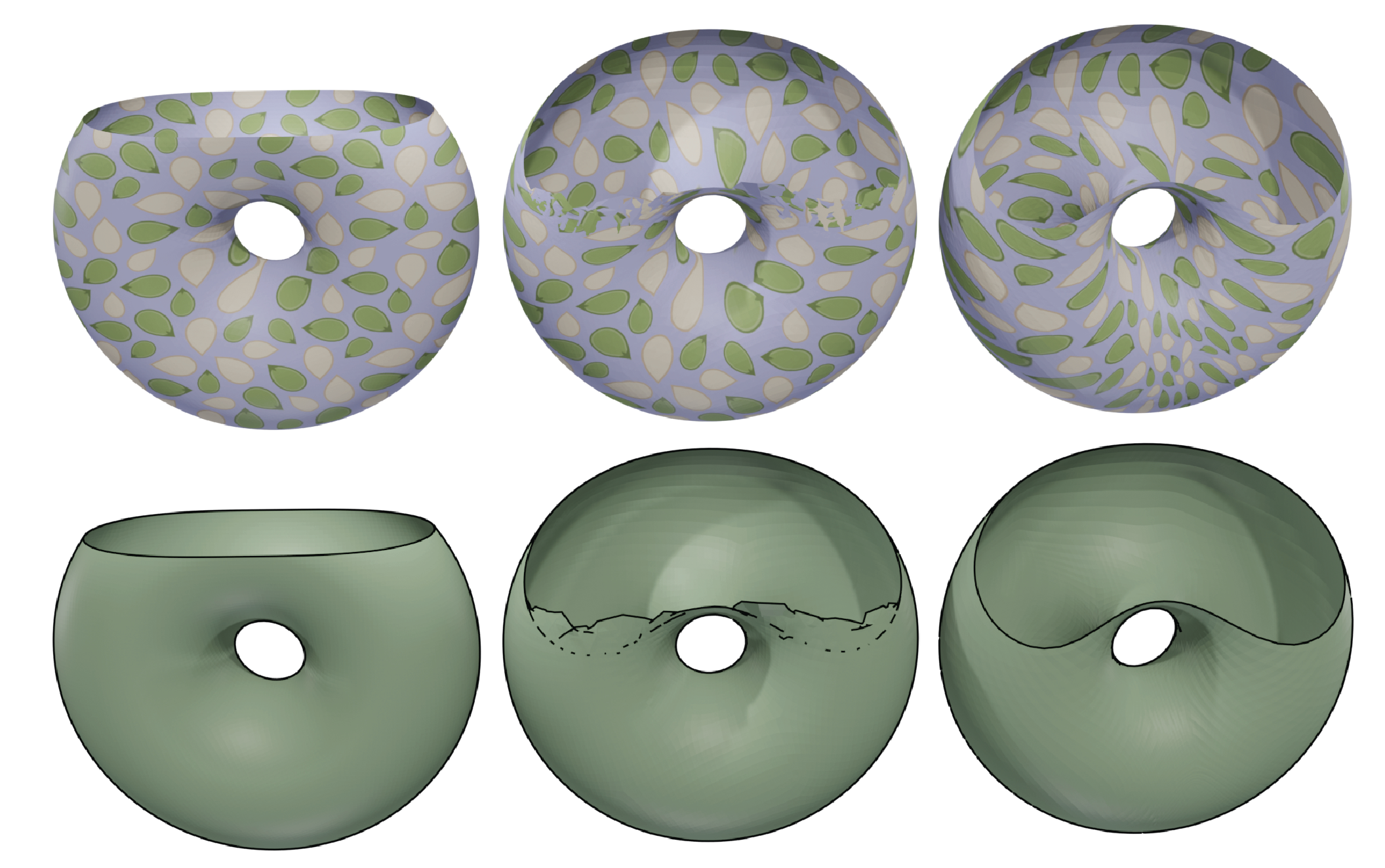
Through this, we are able to produce high-quality quasiconformal mappings without requiring a local parametrization of the surface! Some examples are below.

image-center

A messy implementation of our algorithm can be found on my code page.

Relevant Publications

Anthony Gruber, Eugenio Aulisa. Quasiconformal Mappings for Surface Mesh Optimization. Preprint version available here.

Dr. Anthony Gruber

Relevant Publications